Estadística
Para tener bien claro el concepto de estadística presento 3 conceptos claves para entender muy bien esta ciencia:- es una ciencia formal y una herramienta que estudia el uso y los análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional.
- es un ciencia que utiliza datos numéricos para obtener inferencias basadas en el cálculo de probabilidades.
- es la parte de las matemáticas que se encarga del estudio de una determinada característica en una población, recogiendo los datos, organizándolos en tablas, representándolos gráficamente y analizándolos para sacar conclusiones de dicha población.
Principales Conceptos Relacionados con Estadística
Hablar de estadística, es hablar de:
Población: Es el conjunto formado por todos los elementos a los que les vamos a hacer el estudio
Muestra: Es el subconjunto de la población que elegimos para hacer un estudio más reducido.
Estadistica descriptiva: Realiza el estudio sobre la población completa, observando una característica de la misma y calculando unos parámetros que den información global de toda la población.
Estadistica Inferencial: Realiza el estudio descriptivo sobre un subconjunto de la población llamado muestra y, posteriormente, extiende los resultados obtenidos a toda la población.
Probabilidad: Es una forma de medición de la certidumbre que asociada a la observación u ocurrencia de un fenómeno o al hecho de que una característica de un objeto de estudio adopte cierto valor.
Dato: Son medidas, valores o características susceptibles de ser observados y contados.
Variable: Son caracteres susceptibles a cambio y pueden tener diferentes valores en cada elemento o individuo.
Fenómeno: Se presentan en tiempo y lugar determinado y son ob jetos de estudio y análisis sobre su mayor o menor intensidad de producción. A ellos pertenecen: numéricos, cuanlitativos, geográficos, históricos, típicos y atípicos.
Parámetro: Es una cantidad numerica calculada sobre una población.
Estadistico: Se usa para aproximar un parámetro tambien se suele llamar estimador.
Fenomeno aleatorio: Son aquellos en donde no se sabe con seguridad lo que va a pasar. Estos sucesos dependen del azar.
Fenomeno determinista: Son los hechos o sucesos que ocurren con seguridad. en ellos se conoce de antemano, con certeza, el resultado.
Variable cuantitativa: Es cualquier característica que se puede expresar con números. Por ejemplo, el número de hermanos o la estatura.
Variable cualitativa: Es aquella característica que no podemos expresar con números y hay que expresarla con palabras. Por ejemplo, el lugar de residencia.
Variable continua: Es aquella variable que puede tomar cualquier valor dentro de un intervalo real.
Variable discreta: Es aquella variable que puede tomar únicamente un número finito de valores.
Población finita: Es la que tiene un número extremadamente grande de componentes, como el conjunto de especies que tiene el reino animal.
Población infinita: Es aquella lo bastante grande con relación al sistema de servicio como para que el cambio de tamaño ocasionado por sustracciones o adiciones a la población no afecte significativamente las probabilidades del sistema.
Escala nominal: Sirve para clasificar a los elementos asignandolos a una determinada categoria.
Escala ordinal: es una escala que agrupa objetos medidas y personas en clases o categorias de acuerdo a una caracteristica, atributo o propiedad en estudio, y dispone las clases por orden de su magnitud.
Escala Cardinal: Es aquella que emplea los numeros cardinales y nos permite conocer la distancia entre dos numeros cualesquiera.
Areas del conocimiento cientifico ligadas a la estadística
Sociologia: Se establece la relacion entre estas dos ciencias en el sentido de que la evolucion de la sociedad y todas sus caracteristicas que son conocidas especificamente por la sociologia intercambia necesariamente a las actividades economicas que son parte primordial del estudio de la economía.
Geografia: El desarrollo de los bienes materiales o economicos no podian hacerse efectivos si es que no se contaria con un espacio o con un medio físico adecuado como el que estudia la geografia para poder establecer dicha relación.
Historia: En este campo la relacion se establece en el sentido de que la historia estudia las diferentes formas como a traves del tiempo el hombre a venido adquiriendo sus recursos economicos.
Matematicas: se puede apreciar dicha relacion en el momento en que las matematicas nos permiten representar numericamente los datos que nos proporciona la economia a fin de ser demostrados y analizados.
Metodo cientifico
aqui mostramos los pasos que conlleva el metodo científico.
La estadística y el metodo científico
La Estadística puede definirse como un instrumento del método
científico y por tanto orientado al estudio. Estudiar fenómenos sencillos,
no precisa la utilización de un método estadístico, a pesar de que si
puede aplicarse, no es necesario. Donde aparece la necesidad de
determinar estadísticamente leyes que rigen y permiten explicar
fenómenos y aumentar el conocimiento del ser humano es cuando se
presentan situaciones complejas afectadas por la incertidumbre. Es en
este terreno, en el de la incertidumbre medible, donde la Estadística
encuentra su principal campo de acción.
Estructura para diseñar tablas estadísticas
Estructura para diseñar tablas estadísticas
- Que sea fácil para la audiencia encontrar y entender los números en las tablas.
- Diseñar de manera discreta y sencilla tanto el formato como el título de las tablas, de forma que la atención se centre en los puntos sustanciales expresados por los datos más que en la propia estructura de la tabla.
- En las tablas de presentación, los datos deben presentarse de forma concisa y bien organizada para apoyar el respectivo análisis. Una tabla pequeña bien realizada puede proporcionar una gran cantidad de información que los lectores pueden asimilar rápidamente (recordemos que una de los objetivos del conocimiento científico es su divulgación).
Las tablas se deben presentar en solitario, ya sean publicadas en un informe, un artículo, una publicación o en una página web. Cada tabla debe contener suficientes metadatos, como un título descriptivo y una indicación de la fuente de procedencia, para que pueda ser copiado y pegado en otro documento sin perder su sentido. Si se consigue que las tablas puedan presentarse en solitario, es más probable que sean bien entendidas, ya sea dentro o fuera de su contexto original.Como construir tablas de variables cualitativasTabular datos consiste en confeccionar una tabla en la que aparecen bien organizados los valores de variables que se están estudiando, junto con otros datos que ahora explicamos:- Frecuencia
absoluta (fi) Número de individuos que toma cada valor.
- Frecuencia
relativa (hi): hi = fi/N, resultado de dividir la frecuencia absoluta
entre el total de la población. Da el tanto por uno.
- A diferencia
de las variable cuantitativas no la podemos calcular ni
la Frecuencia absoluta acumulada (Fi), ni Frecuencia
relativa acumulada (Hi), ya que es imposible ordenar de menor a mayor
datos no numéricos
- Los
gráficos se elaborar igual que para las variable cuantitativas.
- Siempre es recomendable hacer la tabla con los porcentajes y la proporción de grados para su representación en los diagramas de sectores. Hay que tener en cuenta que si el diagrama de sectores se dibuja sólo en una semicircuenferencia, habrá que repartir sólo 180º proporcionalmente a todos los datos.
 Forma de construir tablas de frecuencias por intervalosLa distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.Tipos de frecuenciasFrecuencia absolutaLa frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.Se representa por fi.3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.1º Se localizan los valores menor y mayor de la distribución. En este caso son 3 y 48.2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea divisible por el número de intervalos queramos establecer.Es conveniente que el número de intervalos oscile entre 6 y 15.En este caso, 48 - 3 = 45, incrementamos el número hasta 50 : 5 = 10 intervalos.Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
Forma de construir tablas de frecuencias por intervalosLa distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.Tipos de frecuenciasFrecuencia absolutaLa frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.Se representa por fi.3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.1º Se localizan los valores menor y mayor de la distribución. En este caso son 3 y 48.2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea divisible por el número de intervalos queramos establecer.Es conveniente que el número de intervalos oscile entre 6 y 15.En este caso, 48 - 3 = 45, incrementamos el número hasta 50 : 5 = 10 intervalos.Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
Formas Gráficas para representar tablas cualitativas
- La representación gráfica de este tipo de datos está basada en la proporcionalidad de las áreas a las frecuencias absolutas o relativas. Veremos dos tipos de representaciones:
- Diagrama de sectores:
- Diagrama de rectángulos:
- Datos sin agrupar correspondientes a un carácter cuantitativo
- Diagrama de barras:
- Diagrama de frecuencias acumuladas:
- Datos agrupados en intervalos correspondientes a un carácter cuantitativo
- Histograma:
- Polígono de frecuencias acumuladas:
Está representación gráfica consiste en dividir un círculo en tantos sectores circulares como modalidades presente el carácter cualitativo, asignando un ángulo central a cada sector circular proporcional a la frecuencia absoluta ni, consiguiendo de esta manera un sector con área proporcional también a ni.
Así, los ángulos que corresponden a las cuatro modalidades de la tabla adjunta serán:Ejemplo:
Y su representación en un diagrama de sectores será:Número de casos Ángulo(grados) Rehusaron cirugía 26 234° Rehusaron radiación 3 27° Empeoraron por
una enfermedad
ajena al cáncer10 90° Otras causas 1 9°

Esta representación gráfica consiste en construir tantos rectángulos como modalidades presente el carácter cualitativo en estudio, todos ellos con base de igual amplitud. La altura se toma igual a la frecuencia absolua o relativa (según la distribución de frecuencias que estemos representando), consiguiendo de esta manera rectángulos con áreas proporcionales a las frecuencias que se quieren representar.
La representación gráfica de la distribución de frecuencias absolutas del ejemplo anterior será de la forma:Ejemplo: 
Estudiaremos dos tipos de representaciones gráficas, correspondientes a distribuciones de frecuencias (absolutas o relativas) no acumuladas y acumuladas.
Consiste en levantar, para cada valor de la variable, una barra cuya altura sea su frecuencia absoluta o relativa, dependiendo de la distribución de frecuencias que estemos representando.
Así, la representación gráfica de la distribución de frecuencias del ejemplo del nº de hijos será:Ejemplo:

Esta representación gráfica se corresponde con la de una función constante entre cada dos valores de la variable a representar, e igual en cada tramo a la frecuencia relativa acumulada (o absoluta acumulada si se trata de representar una distribución de frecuencias absolutas) hasta el menor de los dos valores de la variable que construyen el tramo en el que es constante.
También para el ejemplo del Número de Hijos, se tendrá un diagrama de frecuencias acumuladas como el del siguiente gráfico:Ejemplo:

Al igual que antes, existen también dos tipos de representaciones gráficas dependiendo de si la distribución de frecuencias en estudio es de datos acumulados o de datos sin acumular.
Al ser esta representación una representación por áreas, hay que distinguir si los intervalos en los que aparecen agrupados los datos son de igualamplitud o no.
Si la amplitud de los intervalos es constante, dicha amplitud puede tomarse como unidad y al ser
Frecuencia (área) = amplitud del intervalo · altura la altura correspondiente a cada intervalo puede tomarse igual a la frecuencia.
Si los intervalos tienen diferente amplitud, se toma alguna de ellas como unidad (generalmente la menor) y se levantan alturas para cada intervalo de forma que la ecuación anterior se cumpla.
En el ejemplo de los Niveles de Colinesterasa, al tener los intervalos igual amplitud, la representación gráfica será:Ejemplo:

Si tuviéramos una distribución de frecuencias como la siguiente, correspondiente a puntuaciones obtenidas en un test psicológico y en la que los intervalos son de diferente amplitudEjemplo:
Tomando la amplitud 5 como unidad, deberemos levantar para el primer intervalo una altura de 2/70 para que el área sea la freceuncia relativa 8/70. Procediendo de la misma manera con el resto de los intervalos obtendríamos como representación gráfica la figura siguiente:Ii ni fi 0-20 8 8/70 20-30 9 9/70 30-40 12 12/70 40-45 10 10/70 45-50 9 9/70 50-60 10 10/70 60-80 8 8/70 80-100 4 4/70 ?ni= 70 ?fi=1

Se utiliza para representar distribuciones de frecuencias (relativas o absolutas) acumuladas. Consiste en representar la gráfica de una función que una por segmentos las alturas correspondientes a los extremos superiores de cada intervalo, tengan o no todos igual amplitud, siendo dicha altura igual a la frecuencia acumulada, dando una altura cero al extremo inferior del primer intervalo y siendo constante a partir del extremo superior del último.
Así, para el ejemplo de los Niveles de Colinesterasa, el polígono de frecuencias relativas acumuladas tendrá una representación gráfica de la forma:Ejemplo:
 Medidas de tendencia centralModa: La moda es el dato más repetido de la encuesta, el valor de la variable con mayor frecuencia absoluta.5 En cierto sentido la definición matemática corresponde con la locución "estar de moda", esto es, ser lo que más se lleva. Su cálculo es extremadamente sencillo, pues solo necesita un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.Media aritmética: es el valor obtenido por la suma de todos sus valores dividida entre el número de sumadores. Es, probablemente, uno de los parámetros estadísticos más extendidos.2 Se le llama también promedio o, simplemente, mediaMediana: es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.7 Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2.Las cuales pueden representarse con estas formulasMedia
Medidas de tendencia centralModa: La moda es el dato más repetido de la encuesta, el valor de la variable con mayor frecuencia absoluta.5 En cierto sentido la definición matemática corresponde con la locución "estar de moda", esto es, ser lo que más se lleva. Su cálculo es extremadamente sencillo, pues solo necesita un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.Media aritmética: es el valor obtenido por la suma de todos sus valores dividida entre el número de sumadores. Es, probablemente, uno de los parámetros estadísticos más extendidos.2 Se le llama también promedio o, simplemente, mediaMediana: es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.7 Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2.Las cuales pueden representarse con estas formulasMedia Moda
Moda Mediana
Mediana Ejemplos-En literatura, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3n = 6
Ejemplos-En literatura, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3n = 6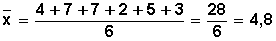 La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.-Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)-Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene: 1, 2, 4, 5, 8, 9, 10El 5 corresponde a la Mediana, porque es el valor central en este conjunto de datos impares.Varianza y desviación estándarDesviación estándarLa desviación estándar (σ) mide cuánto se separan los datos.La fórmula es fácil: es la raíz cuadrada de la varianza.VarianzaLa varianza (que es el cuadrado de la desviación estándar: σ2) se define así:Es la media de las diferencias con la media elevadas al cuadrado.Fórmulas
La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.-Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)-Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene: 1, 2, 4, 5, 8, 9, 10El 5 corresponde a la Mediana, porque es el valor central en este conjunto de datos impares.Varianza y desviación estándarDesviación estándarLa desviación estándar (σ) mide cuánto se separan los datos.La fórmula es fácil: es la raíz cuadrada de la varianza.VarianzaLa varianza (que es el cuadrado de la desviación estándar: σ2) se define así:Es la media de las diferencias con la media elevadas al cuadrado.Fórmulas

 EjemploHallar la desviación media, la varianza y la desviación típica de la series de números siguientes:2, 3, 6, 8, 11.12, 6, 7, 3, 15, 10, 18, 5.2, 3, 6, 8, 11.Media
EjemploHallar la desviación media, la varianza y la desviación típica de la series de números siguientes:2, 3, 6, 8, 11.12, 6, 7, 3, 15, 10, 18, 5.2, 3, 6, 8, 11.Media Varianza
Varianza 12, 6, 7, 3, 15, 10, 18, 5.Media
12, 6, 7, 3, 15, 10, 18, 5.Media Varianza
Varianza
COEFICIENTE DE CORRELACIÓN DE PEARSONEs una medida de la relación lineal entre dos variables aleatorias cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.De manera menos formal, podemos definir el coeficiente de correlación de Pearson como un índice que puede utilizarse para medir el grado de relación de dos variables siempre y cuando ambas sean cuantitativas.FORMULA DE LA COEFICIENTE r DE PEARSON![\rho_{X,Y}={\sigma_{XY} \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y},](http://upload.wikimedia.org/math/2/a/6/2a66d6e8dc4c07c0be10df0b21707ac9.png)
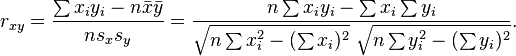 Regresión linealEn estadística la regresión lineal o ajuste lineal es un método matemático que modela la relación entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε.Método de la regresión linealEste modelo puede ser expresado como:
Regresión linealEn estadística la regresión lineal o ajuste lineal es un método matemático que modela la relación entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε.Método de la regresión linealEste modelo puede ser expresado como:
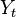 : Variable
dependiente, explicada o regresando.
: Variable
dependiente, explicada o regresando. :
Variables explicativas, independientes o regresares.
:
Variables explicativas, independientes o regresares.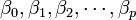 :
Parámetros, miden la influencia que las variables explicativas tienen sobre el
regresando.Donde
:
Parámetros, miden la influencia que las variables explicativas tienen sobre el
regresando.Donde es
la intersección o término "constante", las
es
la intersección o término "constante", las  son
los parámetros respectivos a cada variable independiente, y
son
los parámetros respectivos a cada variable independiente, y  es
el número de parámetros independientes a tener en cuenta en la regresión. La
regresión lineal puede ser contrastada con la regresión no lineal.Problemas resueltosUn centro comercial sabe en función de la distancia, en kilómetros, a la que se sitúe de un núcleo de población, acuden los clientes, en cientos, que figuran en la tabla:
es
el número de parámetros independientes a tener en cuenta en la regresión. La
regresión lineal puede ser contrastada con la regresión no lineal.Problemas resueltosUn centro comercial sabe en función de la distancia, en kilómetros, a la que se sitúe de un núcleo de población, acuden los clientes, en cientos, que figuran en la tabla:Nº de clientes (X) 8 7 6 4 2 1 Distancia (Y) 15 19 25 23 34 40 1. Calcular el coeficiente de correlación lineal.2. Si el centro comercial se sitúa a 2 km, ¿cuántos clientes puede esperar?3. Si desea recibir a 500 clientes, ¿a qué distancia del núcleo de población debe situarse?xi yi xi ·yi xi2 yi2 8 15 120 64 225 7 19 133 49 361 6 25 150 36 625 4 23 92 16 529 2 34 68 4 1 156 1 40 40 1 1 600 28 156 603 170 4 496 



 Correlación negativa muy fuerte.
Correlación negativa muy fuerte.



- Frecuencia
absoluta (fi) Número de individuos que toma cada valor.







 es la
es la 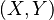
 es la
es la 
 es la
es la 
 a:
a:
No hay comentarios:
Publicar un comentario